|
(考德上师资林耀辉) 牛吃草问题属于一种特殊形式的追及问题,我们在做这类题目时只须把牛吃的速度看作追及问题中追及者的速度,把草的生长速度看作被追及者的速度,实际的消耗速度看作参与追及运动的两个事物之间的相对速度,这样我们就可以很快地理解此类题型并得出公式: 牛吃的速度 — 草长的速度 == 实际消耗速度 举一个最简单的例子: 某牧场原有1000公斤的草,牛群每天吃掉100公斤,而草一天长60公斤,那么把牛群放入该牧场后多少天会吃光所有的草? 根据最简单的数学知识我们知道:
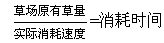
所以这道例题中的消耗时间是:
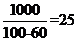
下面我通过一些例题来向大家说明牛吃草问题的基本解题思路。 例1、牧场上长满牧草,每天牧草都匀速生长.这片牧场可供10头牛吃20天,可供15头牛吃10天.供25头牛可吃几天? A.3 B.5 C.7 D.8 考德上师资林耀辉提示:这是一道最常规的牛吃草问题,通过这道题目我希望能让同学们明白牛吃问题设未知数的方法,以及基本解题步骤。 一般地,我们设每头牛每天吃一个单位的草,一共有N头牛,则整个牛群吃草的速度为 N。草场原有草量可供一头牛吃C天,也就是C单位。草的每天生长的量可供一头牛吃G天,换句话说草每天长G单位。消耗时间为T。 那么我们可以很快地列出下式:
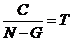
而且我们发现在本题中牧场是恒定的,也就意味着草场原有的草量,以及草的生长速度都是不变的。随着牛的头数发生变化,消耗时间也发生变化。
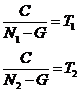
因为草场原有草量是恒定的,据此我们知道消耗速度与消耗时间成反比,可列出下式:
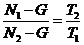
考德上师资林耀辉提示:到这一步我们就可以直接把相关数据代入,再来解分式方程。在这里提醒同学们解分式方程只需方程左右两边分子分母之差相等即可迅速解题,让左右两边分子直接相等。所以我们对方程的右边进行了进一步约分。
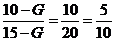
10-G=5 G=5 通过G=5代入公式①我们可以算出C=100。 所以25头牛的消耗时间为:
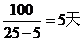
故本题答案选B。 例2、牧场有一片青草,每天生成速度相同。现在这片牧场可供16头牛吃20天,或者供80只羊吃12天,如果一头牛一天吃草量等于4只羊一天的吃草量,那么10头牛与60只羊—起吃可以吃多少天? ( ) A.7 B.8 C.12 D.15 考德上师资林耀辉提示:本题的特点在于有两种吃草的动物,且每种动物吃草速度还不一样。所以我们最好把其中一种动物替换为另一种,这样就回归到牛吃草问题的常见形态了。我建议把羊统统替换为牛,那么每四只羊相当于一头牛。则该题转化为牧场有一片青草,每天生成速度相同。现在这片牧场可供16头牛吃20天,或者供20头牛吃12天,那么25头牛—起吃可以吃多少天? 根据上题所描述的公式我们可以迅速列出:
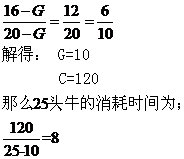
故本题答案选B 例3、如果44头牛吃11公亩牧场的草,14天后可以吃尽,18头牛吃6公亩牧场的草,21天可以吃尽,那么要在24天内吃尽40公亩牧场的草,需要多少头牛(每天长出的草量是相同的)? A 90 B 100 C 110 D 135 考德上师资林耀辉提示:本题的难点在于草场面积发生变化,也就意味着C和G这两个数据不再恒定不变,那么我们解决牛吃草问题的第一组公式(消耗速度与消耗时间成反比)不再成立。在解决这种情况的问题时,我给大家的建议是归一法,就是通过一定的转化,使得每种情况的草场面积都统一到一公亩上,只要草场面积统一,我们就可以用解决牛吃草问题的最常规方法予以解决。所以本题我们可以把它看成如果4头牛吃1公亩牧场的草,14天后可以吃尽,3头牛吃1公亩牧场的草,21天可以吃尽,那么要在24天内吃尽1公亩牧场的草,需要多少头牛? 再问24天内吃尽40公亩牧场的草,需要多少头牛?
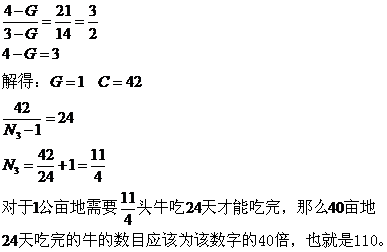
故本题的答案选C。
小编推荐
|



